Performing Complex-valued Linear Transformations using Spatially Incoherent Diffractive Optical Networks

Complex-valued-Linear-Transformations
Complex-valued Linear Transformations using Spatially Incoherent Diffractive Networks (a) The workflow of the spatially incoherent diffractive network model: a complex-valued element of the input vector is represented by a set of real, non-negative intensity values (mosaicing). The resulting input intensity pattern is fed into the incoherent diffractive network. At the output, a complex-valued vector element is synthesized from a predefined set of intensity pixels (demosaicing). (b)Image encryption application. The letters 'U' and 'C' are encoded in the amplitude and phase of a complex image, which is encrypted digitally and thereupon decrypted using the spatially incoherent diffractive network. The decrypted complex image matches the original image very well. Image Credit: Ozcan Lab @ UCLA.

The bulk of the computing in state-of-the-art neural networks comprises linear operations, e.g., matrix-vector multiplications and convolutions. Linear operations can also play an important role in cryptography. While dedicated processors such as GPUs and TPUs are available for performing highly parallel linear operations, these devices are power-hungry, and the low bandwidth of electronics still limits their operation speed. Optics is better suited for such operations because of its inherent parallelism and large bandwidth and computation speed.

Built from a set of spatially engineered thin surfaces, diffractive deep neural networks (D2NN), also known as diffractive networks, form a recently emerging optical computing architecture capable of performing computational tasks passively at the speed of light propagation through an ultra-thin volume. These task-specific all-optical computers are designed digitally through learning of the spatial features of their constituent diffractive surfaces. Following this one-time design process, the optimized surfaces are fabricated and assembled to form the physical hardware of the diffractive optical network.

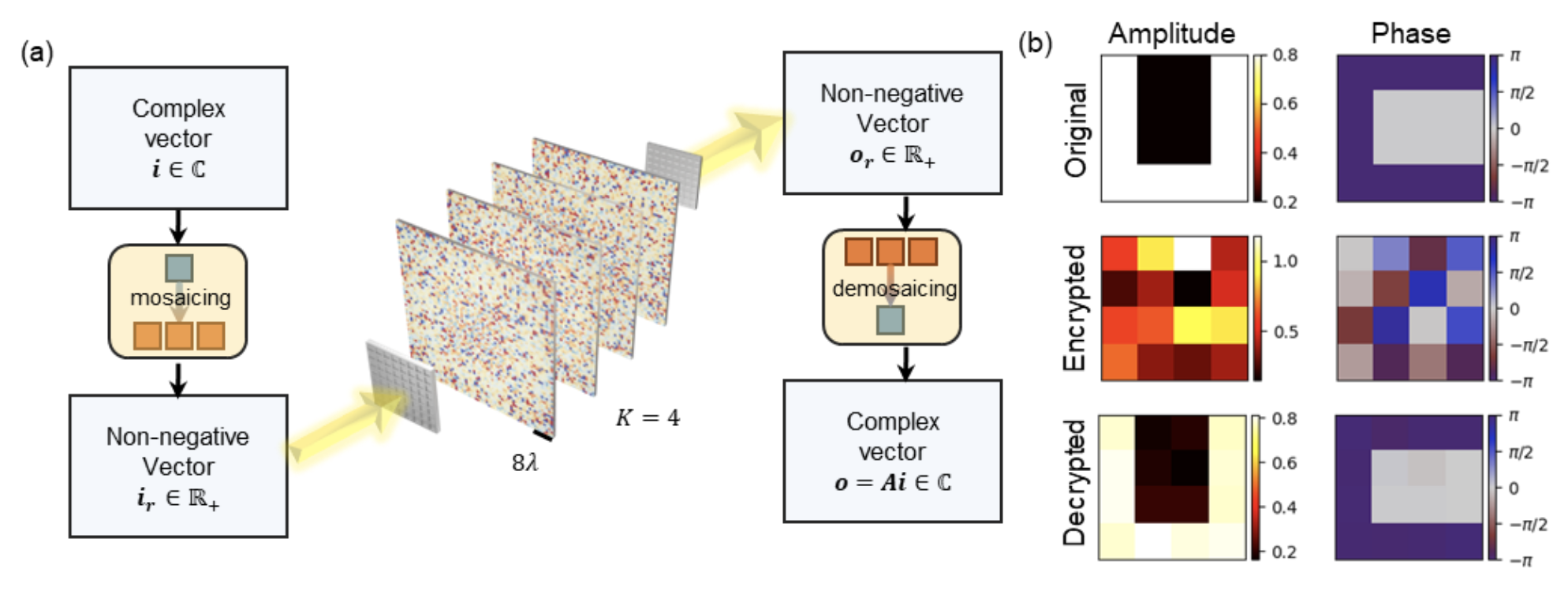
In their recent publication in Advanced Photonics Nexus, a team of researchers led by Aydogan Ozcan, the Chancellor’s Professor and the Volgenau Chair for Engineering Innovation at UCLA, has introduced a method to perform complex-valued linear operations with diffractive networks under spatially incoherent illumination. It had been shown previously by the same group that diffractive networks with sufficient degrees of freedom can perform arbitrary complex-valued linear transformations with spatially coherent light with negligible error. In contrast, with spatially incoherent light, these networks can perform arbitrary linear transformations of input optical intensities if the matrix elements defining the transformation are real and non-negative. Given that spatially incoherent illumination sources are more prevalent and easier to access, there is a growing need for spatially incoherent diffractive processors to handle data beyond just non-negative values.

By incorporating preprocessing and postprocessing steps to represent complex numbers by a set of non-negative real numbers, UCLA researchers have extended the processing power of spatially incoherent diffractive networks to the domain of complex numbers. They demonstrated that such incoherent diffractive processors can be designed to perform an arbitrary complex-valued linear transformation with negligible error if there is a sufficient number of optimizable phase-only diffractive features within the design, which scales with the dimensions of the input and output complex vector spaces.

The researchers showcased the application of this novel scheme via encryption and decryption of complex-valued images using spatially incoherent diffractive networks. Apart from visual image encryption, such spatially incoherent diffractive processors could also be useful in other applications, e.g., in autonomous vehicles for ultra-fast and low-power processing of natural scenes.

See the article:

Xilin Yang, Md Sadman Sakib Rahman, Bijie Bai, Jingxi Li, and Aydogan Ozcan, “Complex-valued universal linear transformations and image encryption using spatially incoherent diffractive networks”, Advanced Photonics Nexus (2023) https://doi.org/10.1117/1.APN.3.1.016010